Answer:
(a)

(b) It is not too low
Explanation:
Given

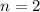
Solving (a):
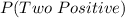
First, calculate the probability of single negative
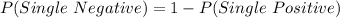 --- complement rule
--- complement rule

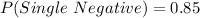
The probability that two combined tests are negative is:
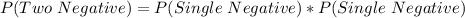
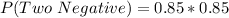
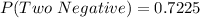
Using the complement rule, we have:

So, we have:
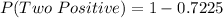

Solving (b): Is (a) low enough?
Generally, when a probability is less than or equal to 0.05; such probabilities are extremely not likely to occur
By comparison:
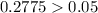
Hence, it is not too low