Question

Suppose a research company takes a random sample of 45 business travelers in the financial industry and determines that the sample average cost of a domestic trip is $1,192, with a sample standard deviation of $279. Construct a 98% confidence interval for the population mean (for domestic trip) from these sample data. Round your answers to 3 decimal places.

Answer 1

98% confidence interval for the population mean =(1095.260,1288.740)

Explanation:

We are given that

n=45

`\mu=1192`

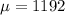
Standard deviation,
`\sigma=279`

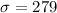
We have to construct a 98% confidence interval for the population mean.

Critical value of z at 98% confidence, Z =2.326

Confidence interval is given by

`(\mu\pm Z(\sigma)/(√(n)))`

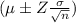
Using the formula

98% confidence interval is given by

`=(1192\pm 2.326* (279)/(√(45)))`

`=(1192\pm 96.740)`

=
`(1192-96.740,1192+96.740)`

=
`(1095.260,1288.740)`

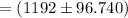
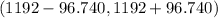
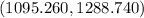
Hence, 98% confidence interval for the population mean (1095.260,1288.740)