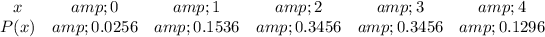Answer:
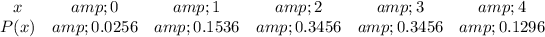
Explanation:
Given
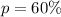
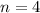
Required
The distribution of x
The above is an illustration of binomial theorem where:
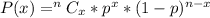
This gives:
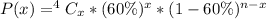
Express percentage as decimal
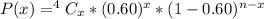
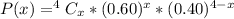
When x = 0, we have:
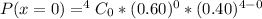
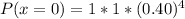
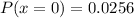
When x = 1
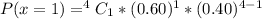
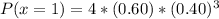
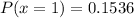
When x = 2
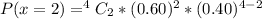
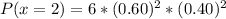
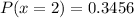
When x = 3
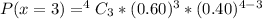
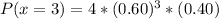
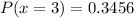
When x = 4
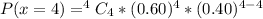
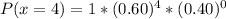
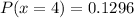
So, the probability distribution is: