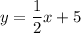Answer:
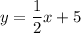
Explanation:
We want to find the slope in slope-intercept form of a line that is parallel to:
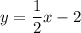
And passes through the point (-8, 1).
Recall that parallel lines have equivalent slopes.
Since the slope of our given line is 1/2, the slope of our new line must also be 1/2.
We are also given that it passes through the point (-8, 1). Since we are given a slope and a point, we can use the point-slope form:
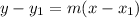
Substitute 1/2 for m and (-8, 1) for (x₁, y₁). Hence:
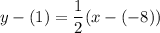
Since we want the equation in slope-intercept form, we can isolate y. Distribute:
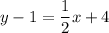
Therefore, our equation is: