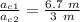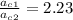Question

The large blade of a helicopter is rotating in a horizontal circle. The length of the blade is 6. 7 m, measured from its tip to the center of the circle. Find the ratio of the centripetal acceleration at the end of the blade to that which exists at a point located 3.0 m from the center of the circle.

Answer 1

`(a_(c1))/(a_(c2)) = 2.23`

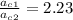
Step-by-step explanation:

The centripetal acceleration is given as follows:

`a_c = (v^2)/(r)\\`

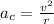
where,

ac = centripetal acceleration

v = linear speed = rω

r = radius

ω = angular speed

Therefore,

`a_c = ((r\omega)^2)/(r)\\\\a_c = r\omega^2`

Therefore, the ratio will be:

`(a_(c1))/(a_(c2)) = (r_1\omega^2)/(r_2\omega^2)\\\\(a_(c1))/(a_(c2)) = (r_1)/(r_2)\\\\`

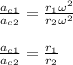
where,

r₁ = 6.7 m

r₂ = 3 m

Therefore,

`(a_(c1))/(a_(c2)) = (6.7\ m)/(3\ m)\\\\`

`(a_(c1))/(a_(c2)) = 2.23`