1 Answer

Amadiere · Answer 1 · 2022-02-22T23:13:34+0000

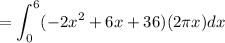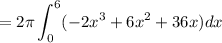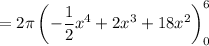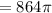$V = 864\pi$

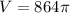
Explanation:

Since one of the boundaries is y = 0, we need to find the roots of the function
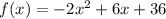f(x)=-2x^2+6x+36 . Using the quadratic equation, we get

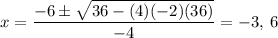
$x = (-6 \pm √(36 - (4)(-2)(36)))/(-4)= -3,\:6$

But since the region is also bounded by
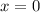x = 0 , that means that our limits of integration are from
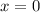x=0 (instead of -3) to
x=6 .

Now let's find the volume using the cylindrical shells method. The volume of rotation of the region is given by

$\displaystyle V = \int f(x)2\pi xdx$

$\:\:\:\:\:\:\:= \displaystyle \int_0^6 (-2x^2+6x+36)(2 \pi x)dx$

$\:\:\:\:\:\:\:= \displaystyle 2\pi \int_0^6 (-2x^3+6x^2+36x)dx$

$\:\:\:\:\:\:\:= \displaystyle 2\pi \left(-(1)/(2)x^4+2x^3+18x^2 \right)_0^6$

$\:\:\:\:\:\:\:= 864\pi$

Please log in or register to add a comment.