Question

Determine if a quadrilateral with the given vertices is an isosceles trapezoid. Show and explain all steps to prove or disprove.

A(3, 3) B(5, 3) C(8,1) D(1,1)

Answer 1

No, a quadrilateral with the given vertices is not an isosceles trapezoid.

Explanation:

We are given that

A(3,3), B(5,3), C(8,1), D(1,1)

Slope formula:

`m=(y_2-y_1)/(x_2-x_1)`

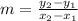
Slope of AB=
`(3-3)/(5-3)=0`

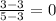
Slope of BC=
`(1-3)/(8-5)=(-2)/(3)`

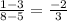
Slope of CD=
`(1-1)/(1-8)=0`

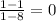
Slope of AD=
`(1-3)/(1-3)=1`

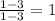
Slope of AB=Slope of CD

When slopes of two lines are equal then the lines are parallel.

Therefore, AB is parallel to CD.

When one pair of quadrilateral is parallel then the quadrilateral is trapezoid.

`\implies`ABCD is a trapezoid.

Distance formula:

`√((x_2-x_1)^2+(y_2-y_1)^2)`

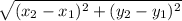
Using the formula

Length of BC=
`√((8-5)^2+(1-3)^2)`

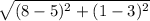
Length of BC=
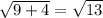`√(9+4)=√(13)` units

Length of AD=
`√((1-3)^2+(1-3)^2)`

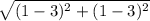
Length of AD=
`√(4+4)=2√(2)`

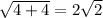
Length of AD is not equal to length of BC.

Hence, trapezoid is not an isosceles trapezoid.