Assuming the probability of a single sample testing positive is 0.15, find the probability of a positive result for two samples combined into one mixture. Is the probability lo…

Question

asked Jan 26, 2022 46.7k views

1 Answer

Smrutiranjan Sahu · Answer 1 · 2022-02-02T03:08:29+0000

Answer:

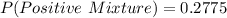
$P(Positive\ Mixture) = 0.2775$

The probability is not low

Explanation:

Given

$P(Single\ Positive) = 0.15$

n = 2

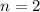
Required

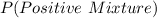
$P(Positive\ Mixture)$

First, we calculate the probability of single negative using the complement rule

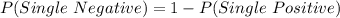
$P(Single\ Negative) = 1 - P(Single\ Positive)$

$P(Single\ Negative) = 1 - 0.15$

$P(Single\ Negative) = 0.85$

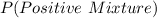$P(Positive\ Mixture)$ is calculated using:

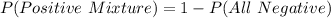$P(Positive\ Mixture) = 1 - P(All\ Negative)$ ---- i.e. complement rule

So, we have:

$P(Positive\ Mixture) = 1 - 0.85^2$

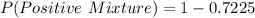
$P(Positive\ Mixture) = 1 - 0.7225$

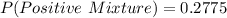
$P(Positive\ Mixture) = 0.2775$

Probabilities less than 0.05 are considered low.

So, we can consider that the probability is not low because 0.2775 > 0.05