Question

The radius of a right circular cone is increasing at a rate of 1.4 in/s while its height is decreasing at a rate of 2.4 in/s. At what rate is the volume of the cone changing when the radius is 140 in. and the height is 186 in.

Answer 1

The volume is increasing at a rate of 27093 cubic inches per second.

Explanation:

Volume of a cone:

THe volume of a cone, with radius r and height h, is given by:

`V = (1)/(3) \pi r^2h`

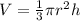
In this question:

We have to differentiate implictly is function of t, so the three variables, V, r and h, are differenciated. So

`(dV)/(dt) = (\pi r^2)/(3)(dh)/(dt) + (2\pi rh)/(3)(dr)/(dt)`

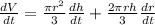
The radius of a right circular cone is increasing at a rate of 1.4 in/s while its height is decreasing at a rate of 2.4 in/s.

This means that
`(dr)/(dt) = 1.4, (dh)/(dt) = -2.4`

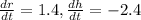
Radius is 140 in. and the height is 186 in.

This means that
`r = 140, h = 186`

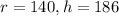
At what rate is the volume of the cone changing?

`(dV)/(dt) = (\pi r^2)/(3)(dh)/(dt) + (2\pi rh)/(3)(dr)/(dt)`

`(dV)/(dt) = (\pi (140)^2)/(3)(-2.4) + (2\pi 140*186)/(3)1.4`

`(dV)/(dt) = -0.8\pi(140)^2 + 62*2\pi*1.4*140`

`(dV)/(dt) = 27093`

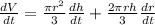
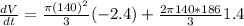
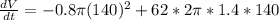
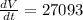
Positive, so increasing.

The volume is increasing at a rate of 27093 cubic inches per second.