Question

In how many ways can we seat 3 pairs of siblings in a row of 7 chairs, so that nobody sits next to their sibling

Answer 1

1,968

Explanation:

Let x₁ and x₂, y₁ and y₂, and z₁ and z₂ represent the 3 pairs of siblings, and let;

Set X represent the set where the siblings x₁ and x₂ sit together

Set Y represent the set where the siblings y₁ and y₂ sit together

Set Z represent the set where the siblings z₁ and z₂ sit together

We have;

Where the three siblings don't sit together given as
`X^c`∩
`Y^c`∩
`Z^c`

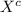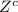
By set theory, we have;

`\left | X^c \cap Y^c \cap Z^c \right |` =
`\left | X^c \cup Y^c \cup Z^c \right |` =
`\left | U \right | - \left | X \cup Y \cup Z \right |`

`\left | U \right | - \left | X \cup Y \cup Z \right |` =
`\left | U \right | - \left (\left | X \right | + \left | Y\right | + \left | Z\right | - \left | X \cap Y\right | - \left | X \cap Z\right | - \left | Y\cap Z\right | + \left | X \cap Y \cap Z\right | \right)`

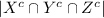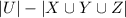
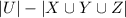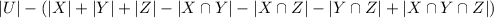
Therefore;

`\left | X^c \cap Y^c \cap Z^c \right | = \left | U \right | - \left (\left | X \right | + \left | Y\right | + \left | Z\right | - \left | X \cap Y\right | - \left | X \cap Z\right | - \left | Y\cap Z\right | + \left | X \cap Y \cap Z\right | \right)`

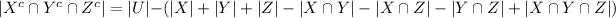
Where;

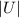`\left | U\right |` = The number of ways the 3 pairs of siblings can sit on the 7 chairs = 7!

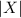`\left | X\right |` = The number of ways x₁ and x₂ can sit together on the 7 chairs = 2 × 6!

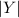`\left | Y\right |` = The number of ways y₁ and y₂ can sit together on the 7 chairs = 2 × 6!

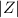`\left | Z\right |` = The number of ways z₁ and z₂ can sit together on the 7 chairs = 2 × 6!

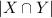`\left | X \cap Y\right |` = The number of ways x₁ and x₂ and y₁ and y₂ can sit together on the 7 chairs = 2 × 2 × 5!

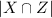`\left | X \cap Z\right |` = The number of ways x₁ and x₂ and z₁ and z₂ can sit together on the 7 chairs = 2 × 2 × 5!

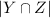`\left | Y \cap Z\right |` = The number of ways y₁ and y₂ and z₁ and z₂ can sit together on the 7 chairs = 2 × 2 × 5!

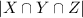`\left | X \cap Y \cap Z\right |` = The number of ways x₁ and x₂, y₁ and y₂ and z₁ and z₂ can sit together on the 7 chairs = 2 × 2 × 2 × 4!

Therefore, we get;

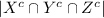`\left | X^c \cap Y^c \cap Z^c \right |` = 7! - (2×6! + 2×6! + 2×6! - 2 × 2 × 5! - 2 × 2 × 5! - 2 × 2 × 5! + 2 × 2 × 2 × 4!)

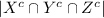`\left | X^c \cap Y^c \cap Z^c \right |` = 5,040 - 3072 = 1,968

The number of ways where the three siblings don't sit together given as
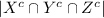`\left | X^c \cap Y^c \cap Z^c \right |` = 1,968