Answer:
0.5015 = 50.15% probability that it came from manufacturer A.
Explanation:
Conditional Probability
We use the conditional probability formula to solve this question. It is

In which
P(B|A) is the probability of event B happening, given that A happened.
 is the probability of both A and B happening.
is the probability of both A and B happening.
P(A) is the probability of A happening.
In this question:
Event A: Defective
Event B: From manufacturer A.
Probability a unit is defective:
2% of 43%(from manufacturer A)
1.5% of 57%(from manufacturer B). So

Probability a unit is defective and from manufacturer A:
2% of 43%. So
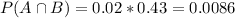
What is the probability that it came from manufacturer A?
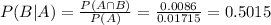
0.5015 = 50.15% probability that it came from manufacturer A.