Question

If 5.4 J of work is needed to stretch a spring from 15 cm to 21 cm and another 9 J is needed to stretch it from 21 cm to 27 cm, what is the natural length (in cm) of the spring

Answer 1

the natural length of the spring is 9 cm

Step-by-step explanation:

let the natural length of the spring = L

For each of the work done, we set up an integral equation;

`5.4 = \int\limits^(21-l)_(15-l) {kx} \, dx \\\\5.4 = [(1)/(2)kx^2 ]^(21-l)_(15-l)\\\\5.4 = (k)/(2) [(21-l)^2 - (15-l)^2]\\\\k = (2(5.4))/((21-l)^2 - (15-l)^2) \ \ \ -----(1)`

The second equation of work done is set up as follows;

`9 = \int\limits^(27-l)_(21-l) {kx} \, dx \\\\9 = [(1)/(2)kx^2 ]^(27-l)_(21-l)\\\\9 = (k)/(2) [(27-l)^2 - (21-l)^2] \\\\k = (2(9))/((27-l)^2 - (21-l)^2) \ \ \ -----(2)`

solve equation (1) and equation (2) together;

`(2(9))/((27-l)^2 - (21-l)^2) = (2(5.4))/((21-l)^2 - (15-l)^2)\\\\(2(9))/(2(5.4)) = ((27-l)^2 - (21-l)^2)/((21-l)^2 - (15-l)^2)\\\\(9)/(5.4) = ((729 - 54l+ l^2) - (441-42l+ l^2))/((441-42l+ l^2) - (225 -30l+ l^2)) \\\\(9)/(5.4 ) = (288-12l)/(216-12l) \\\\(9)/(5.4 ) =(12)/(12) ((24-l)/(18 -l))\\\\(9)/(5.4 ) = (24-l)/(18 -l)\\\\9(18-l) = 5.4(24-l)\\\\162-9l = 129.6-5.4l\\\\162-129.6 = 9l - 5.4 l\\\\32.4 = 3.6 l\\\\l = (32.4)/(3.6) \\\\`

`l = 9 \ cm`

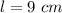
Therefore, the natural length of the spring is 9 cm