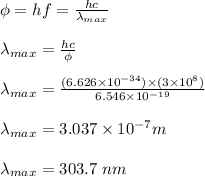Question

When UV light of wavelength 248 nm is shone on aluminum metal, electrons are ejected withmaximum kinetic energy 0.92 eV. What maximum wavelength of light could be used to ejectelectrons from aluminum

Answer 1

The maximum wavelength of light that could liberate electrons from the aluminum metal is 303.7 nm

Step-by-step explanation:

Given;

wavelength of the UV light, λ = 248 nm = 248 x 10⁻⁹ m

maximum kinetic energy of the ejected electron, K.E = 0.92 eV

let the work function of the aluminum metal = Ф

Apply photoelectric equation:

E = K.E + Ф

Where;

Ф is the minimum energy needed to eject electron the aluminum metal

E is the energy of the incident light

The energy of the incident light is calculated as follows;

`E = hf = h(c)/(\lambda) \\\\where;\\\\h \ is \ Planck's \ constant = 6.626 * 10^(-34) \ Js\\\\c \ is \ speed \ of \ light = 3 * 10^(8) \ m/s\\\\E = ((6.626* 10^(-34))* (3* 10^8))/(248* 10^(-9)) \\\\E = 8.02 * 10^(-19) \ J`

The work function of the aluminum metal is calculated as;

Ф = E - K.E

Ф = 8.02 x 10⁻¹⁹ - (0.92 x 1.602 x 10⁻¹⁹)

Ф = 8.02 x 10⁻¹⁹ J - 1.474 x 10⁻¹⁹ J

Ф = 6.546 x 10⁻¹⁹ J

The maximum wavelength of light that could liberate electrons from the aluminum metal is calculated as;

`\phi = hf = (hc)/(\lambda_(max)) \\\\\lambda_(max) = (hc)/(\phi) \\\\\lambda_(max) = ((6.626* 10^(-34)) * (3 * 10^8) )/(6.546 * 10^(-19)) \\\\\lambda_(max) = 3.037 * 10^(-7) m\\\\\lambda_(max) = 303.7 \ nm`