Question

Your boss wants you to advise him about what shape of wheels to use for his son’s pinewood

derby. This is where a car is released from rest and rolls down the ramp to the finish line under
the influence of gravity. He was thinking of using heavy tungsten wheels with most of the weight
in a hoop shape. Explain to him that a solid sphere will go faster at the bottom than a hoop by what amount?

Answer 1

Ring v² = gh

solid wheel (cylinder) v² = 4/3 gh

Step-by-step explanation:

Let's use conservation of energy to find the speed of the wheels at the bottom of the hill.

starting point. Point before starting movement

Em₀ = mgh

final point. At the bottom of the hill

Em_f = K = ½ m v² + ½ I w²

energy is conserved

Emo = Em_f

mgh = ½ m v² + ½ I w²

angular and linear velocity are related

v = w r

we substitute

mgh = ½ m v² + ½ I v² / r²

mgh =
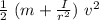`(1)/(2) \ ( m+ (I)/(r^2) ) \ v^2`½ (m + I / r²) v²

v² =
`(2mgh)/(m+ (I)/(r^2) )`

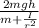
the moments of inertia are tabulated

Ring

I = mr²

v² = 2 m g h / (m + m)

v² = gh

solid wheel (cylinder)

I = ½ m r²

v² = 2m gh / (m + m / 2)

v² = 4/3 gh

We can see that due to the difference in the moment of inertia of each body it is different, the solid wheel has more speed when it reaches the lower part of the ramp