Question

Suppose 58% of the population has a retirement account. If a random sample of size 570 is selected, what is the probability that the proportion of persons with a retirement account will be less than 57%

Answer 1

The probability that the proportion of persons with a retirement account will be less than 57%=31.561%

Explanation:

We are given that

n=570

p=58%=0.58

We have to find the probability that the proportion of persons with a retirement account will be less than 57%.

q=1-p=1-0.58=0.42

By takin normal approximation to binomial then sampling distribution of sample proportion follow normal distribution.

Therefore,
`\hat{p}\sim N(\mu,\sigma^2)`

`\mu_{\hat{p}}=p=0.58`

`\sigma_{\hat{p}}=\sqrt{(p(1-p))/(n)}`

`\sigma_{\hat{p}}=\sqrt{(0.58* 0.42)/(570)}`

`\sigma_{\hat{p}}=0.02067`

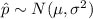
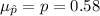
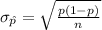
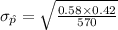
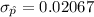
Now,

`P(\hat{p}<0.57)=P(\frac{\hat{p}-\mu_{\hat{p}}}{\sigma_{\hat{p}}}<(0.57-0.58)/(0.02067))`

`P(\hat{p}<0.57)=P(Z<-0.483)`

`P(\hat{p}<0.57)=0.31561* 100`

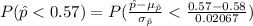
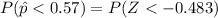
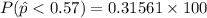
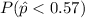`P(\hat{p}<0.57)`=31.561%

Hence, the probability that the proportion of persons with a retirement account will be less than 57%=31.561%