Question

In a randomly selected sample of 100 students at a University, 81 of them had access to a computer at home. Give the value of the standard error for the point estimate.

Answer 1

The value of the standard error for the point estimate is of 0.0392.

Explanation:

Central Limit Theorem

The Central Limit Theorem establishes that, for a normally distributed random variable X, with mean
`\mu` and standard deviation
`\sigma`, the sampling distribution of the sample means with size n can be approximated to a normal distribution with mean
`\mu` and standard deviation
`s = (\sigma)/(√(n))`.

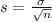For a skewed variable, the Central Limit Theorem can also be applied, as long as n is at least 30.

For a proportion p in a sample of size n, the sampling distribution of the sample proportion will be approximately normal with mean
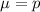`\mu = p` and standard deviation
`s = \sqrt{(p(1-p))/(n)}`

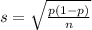
In a randomly selected sample of 100 students at a University, 81 of them had access to a computer at home.

This means that
`n = 100, p = (81)/(100) = 0.81`

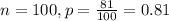
Give the value of the standard error for the point estimate.

This is s. So

`s = \sqrt{(0.81*0.19)/(100)} = 0.0392`

The value of the standard error for the point estimate is of 0.0392.