The quadratic function f has a vertex at (3,4) and opens upward. The quadratic function g is shown below. Which statement is true? A. The minimum value of g is greater than the …

Question

asked Apr 18, 2022 3.1k views

2 Answers

Gaston Sanchez · Answer 1 · 2022-04-20T06:56:21+0000

Answer:

The minimum value of f(x) is greater than the minimum value of g(x).

Explanation:

Given

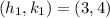(h_1,k_1) = (3,4) --- vertex of f(x)

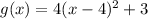g(x) = 4(x - 4)^2 + 3 --- g(x) equation

Required

Which of the options is true

First, we identify the vertex of g(x)

A quadratic function is represented as:

g(x) =a(x - h)^2 + k

Where:

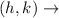$(h,k) \to$ vertex

So, we have:

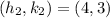
(h_2,k_2) = (4,3)

a = 4

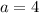
If
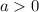a>0 , then the curve opens upward

From the question, we understand that f(x) also open upward. This means that both functions have a minimum

The minimum is the y (or k) coordinate

So, we have:

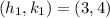(h_1,k_1) = (3,4) --- vertex of f(x)

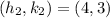(h_2,k_2) = (4,3) --- vertex of g(x)

The minimum of both are:

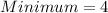Minimum = 4 ---- f(x)

Minimum = 3 ---- g(x)

By comparison:

4 > 3

Hence, f(x) has a greater minimum