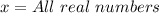Question

I need help nowww!! 16 points

Answer 1

A: x = 0

B: x = All real numbers

Explanation:

A.

Any number to the power of (0) equals one. This applies true for the given situation; one is given an expression which is as follows;

`(6^2)^x=1`

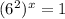
Simplifying that will result in;

`36^x=1`

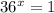
As stated above, any number to the power of (0) equals (1), thus (x) must equal (0) for this equation to hold true.

`36^0=1\\x=0`

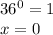
B.

As stated in part (A), any number to the power (0) equals (1). Therefore, when given the following expression;

`(6^0)^x=1`

One can simplify that;

`1^x=1`

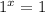
However, (1) to any degree still equals (1). Thus, (x) can be any value, and the equation will still hold true.

`x=All\ real \ numbers`