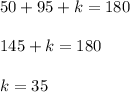Answer:
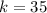 °
°
Explanation:
The degree measure of a straight line is (180) degrees. Therefore, when a line intersects another line, the sum of angle measures on any one side of the line is (180). One can apply this here to find the supplement (the angle on the same side of the line) of the angle with a measure of (130) degrees, and (85) degrees.
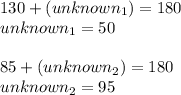
The sum of angle measures in a triangle is (180) degrees, one can apply this here by stating the following;
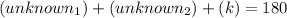
Substitute,
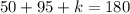
Simplify,