Question

Q.1 Determine whether y = (c - e ^ x)/(2x); y^ prime =- 2y+e^ x 2x is a solution for the differential equation Q.2 Solve the Initial value problem ln(y ^ x) * (dy)/(dx) = 3x ^ 2 * y given y(2) = e ^ 3 . Q.3 Find the general solution for the given differential equation. (dy)/(dx) = (2x - y)/(x - 2y)

Answer 1

(Q.1)

`y = (C - e^x)/(2x) \implies y' = (-2xe^x-2C+2e^x)/(4x^2) = (-xe^x-C+e^x)/(2x^2)`

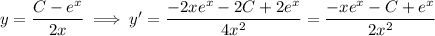
Then substituting into the DE gives

`(-xe^x-C+e^x)/(2x^2) = -(2\left((C-e^x)/(2x)\right) + e^x)/(2x)`

`(-xe^x-C+e^x)/(2x^2) = -(C-e^x + xe^x)/(2x^2)`

`(-xe^x-C+e^x)/(2x^2) = (-C+e^x - xe^x)/(2x^2)`

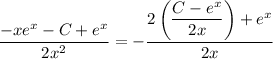
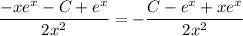
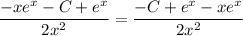
and both sides match, so y is indeed a valid solution.

(Q.2)

`\ln\left(y^x\right)(\mathrm dy)/(\mathrm dx) = 3x^2y`

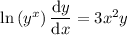
This DE is separable, since you can write
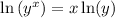`\ln\left(y^x\right)=x\ln(y)`. So you have

`x\ln(y)(\mathrm dy)/(\mathrm dx) = 3x^2y`

`\frac{\ln(y)}y\,\mathrm dy = 3x\,\mathrm dx`

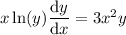
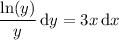
Integrate both sides (on the left, the numerator suggests a substitution):

`\frac12 \ln^2(y) = \frac32 x^2 + C`

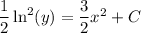
Given y (2) = e ³, we find

`\frac12 \ln^2(e^3) = 6 + C`

`C = \frac12 *3^2 - 6 = -\frac32`

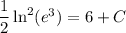
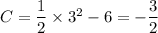
so that the particular solution is

`\frac12 \ln^2(y) = \frac32 x^2 - \frac32`

`\ln(y) = \pm√(3x^2 - 3)`

`\boxed{y = e^(\pm√(3x^2-3))}`

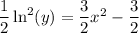
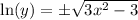
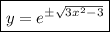
(Q.3) I believe I've already covered in another question you posted.