Answer:
0.2209 = 22.09% probability that in a randomly selected office hour, the number of student arrivals is 3.
Explanation:
We have the mean during an interval, so the Poisson distribution is used.
Poisson distribution:
In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

In which
x is the number of sucesses
e = 2.71828 is the Euler number
 is the mean in the given interval.
is the mean in the given interval.
A statistics professor finds that when she schedules an office hour for student help, an average of 3.3 students arrive.
This means that
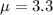
Find the probability that in a randomly selected office hour, the number of student arrivals is 3.
This is P(X = 3). So

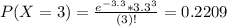
0.2209 = 22.09% probability that in a randomly selected office hour, the number of student arrivals is 3.