Answer:
The t-value for this data is -4.
The p-value of the test is 0.0003 < 0.05, which means that the null hypothesis can be rejected.
Explanation:
College national study finds that students buy coffee from a coffee shop on average 12 times a week, I believe it may be different for UML students.
At the null hypothesis, we test if the mean is of 12, that is:
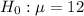
At the alternative hypothesis, we test if the mean is different of 12, that is:
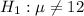
The test statistic is:
We have the standard deviation for the sample, so the t-distribution is used to solve this question.

In which X is the sample mean,
 is the value tested at the null hypothesis, s is the standard deviation and n is the size of the sample.
is the value tested at the null hypothesis, s is the standard deviation and n is the size of the sample.
12 is tested at the null hypothesis:
This means that
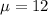
I collect data from a sample of 36 UML students and find that they buy coffee on average 8 times a week, with a standard deviation of 6 days.
This means that
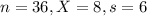
Value of the test statistic:

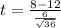
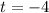
The t-value for this data is -4.
P-value of the test:
Considering a standard significance level of 0.05.
Test if the mean is different from a value, so two-tailed test, with 36 - 1 = 35 df and t = -4. Using a t-distribution calculator, the p-value is of 0.0003.
The p-value of the test is 0.0003 < 0.05, which means that the null hypothesis can be rejected.