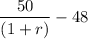Question

You have been asked to create a synthetic short position in a forward contract that permits you to sell 10 units of the underlying one year from now at a price of $50 per unit. (1) Describe the positions you need to take in call and put options to achieve the synthetic short forward position. (2) If the underlying is selling for $48 today (i.e. So = 48), what is the cost of your synthetic short position?

Answer 1

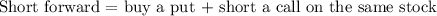`\text{Short forward = buy a put + short a call on the same stock}` with the same exercise price.

X = exercise price = 50

1). Position to be taken :

-- buy 10 numbers of Put options with strike price of $ 50 per unit.

--- short (sell) 10 numbers of Call option with strike price of $ 50 per unit.

2). Cost of synthetic short position =
`$10 * (P-C)$`,

where, P = price of 1 put ption

C = price of 1 call option

The Call - Put parity equation :

`$(C+X)/((1+r)^t)=S_0+P$`

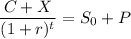
Here, C = Call premium

X = strike price of call and Put

r = annual rate of interest

t = time in years

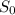`$S_0$` = initial price of underlying

P = Put premium

Therefore,

`$P-C=PV(X)-S_0=(X)/((1+r)^t)-S_0$`

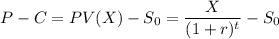
Here, t = 1,
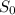`S_0` = 48, X = 50

So the cost of the position is given as :
`$(50)/((1+r)) -48$`