Question

A textile fiber manufacturer is investigating a new drapery yarn, which the company claims has a mean thread elongation of 12 kilograms with a standard deviation of 0.5 kilograms. The company wishes to test the hypothesis H0: µ = 12 against H1: µ < 12 using a random sample of n = 4 specimens. Calculate the P-value if the observed statistic is Xbar (average) = 11.25. Suppose that the distribution of the sample mean is approximately normal.

Answer 1

The p-value of the test is 0.0013.

Explanation:

The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

12 is tested at the null hypothesis:

This means that
`\mu = 12`

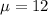
Standard deviation of 0.5 kilograms.

This means that
`\sigma = 0.5`

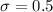
Sample of n = 4 specimens. Observed statistic is Xbar (average) = 11.25.

This means that
`n = 4, X = 11.25`

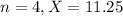
Value of the test statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (11.25 - 12)/((0.5)/(√(4)))`

`z = -3`

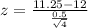
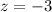
P-value:

Probability of finding a sample mean belo 11.25, which is the p-value of z = -3.

Looking at the z-table, z = -3 has a p-value of 0.0013, thus the this is the p-value of the test.