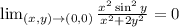Answer:
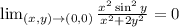
Explanation:
Given
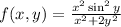
Required
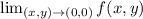
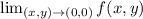 becomes
becomes
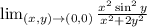
Multiply by 1
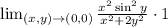
Express 1 as
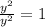
So, the expression becomes:
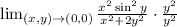
Rewrite as:
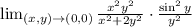
In limits:
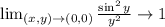
So, we have:
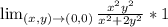
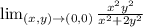
Convert to polar coordinates; such that:
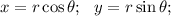
So, we have:
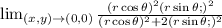
Expand
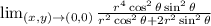
Factor out
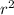
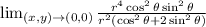
Cancel out
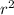
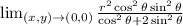
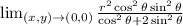
Express
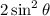 as
as
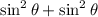
So:
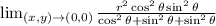
In trigonometry:
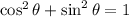
So, we have:
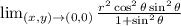
Evaluate the limits by substituting 0 for r
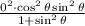
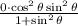
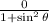
Since the denominator is non-zero; Then, the expression becomes 0 i.e.
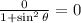
So,