Question

asked Aug 9, 2022 120k views

1 Answer

Zwirbelbart · Answer 1 · 2022-08-14T09:31:14+0000

Answer:

0.319 = 31.9% probability that the wait time will be more than an additional 16 minutes

Explanation:

To solve this question, we need to understand the exponential distribution and conditional probability.

Exponential distribution:

The exponential probability distribution, with mean m, is described by the following equation:

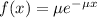
$f(x) = \mu e^(-\mu x)$

In which
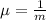$\mu = (1)/(m)$ is the decay parameter.

The probability that x is lower or equal to a is given by:

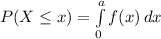
$P(X \leq x) = \int\limits^a_0 {f(x)} \, dx$

Which has the following solution:

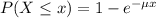
$P(X \leq x) = 1 - e^(-\mu x)$

The probability of finding a value higher than x is:

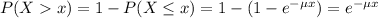
$P(X > x) = 1 - P(X \leq x) = 1 - (1 - e^(-\mu x)) = e^(-\mu x)$

Conditional Probability

We use the conditional probability formula to solve this question. It is

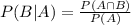
$P(B|A) = (P(A \cap B))/(P(A))$

In which

P(B|A) is the probability of event B happening, given that A happened.

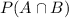$P(A \cap B)$ is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

Event A: It has already taken 11 minutes.

Event B: It will take 16 more minutes.

Exponentially distributed with an average wait time of 14 minutes.

This means that
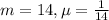
$m = 14, \mu = (1)/(14)$

Probability of the waiting time being of at least 11 minutes:

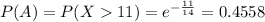
$P(A) = P(X > 11) = e^{-(11)/(14)} = 0.4558$

Probability of the waiting time being of at least 11 minutes, and more than an additional 16 minutes:

More than 11 + 16 = 27 minutes. So

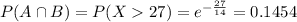
$P(A \cap B) = P(X > 27) = e^{-(27)/(14)} = 0.1454$

What is the probability that the wait time will be more than an additional 16 minutes?

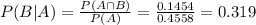
$P(B|A) = (P(A \cap B))/(P(A)) = (0.1454)/(0.4558) = 0.319$

0.319 = 31.9% probability that the wait time will be more than an additional 16 minutes

Please log in or register to add a comment.