Question

Find all relative extrema of the function. Use the Second Derivative Test where applicable. (If an answer does not exist, enter DNE.)

f(x) = x² + 5x – 2

relative maximum
(x, y) = DNE


relativo minimum
(x, y) =

Answer 1

Relative minimum:
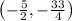`\left(-(5)/(2), -(33)/(4)\right)`, Relative maximum:
`DNE`

Explanation:

First, we obtain the First and Second Derivatives of the polynomic function:

First Derivative

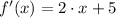`f'(x) = 2\cdot x + 5` (1)

Second Derivative

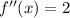`f''(x) = 2` (2)

Now, we proceed with the First Derivative Test on (1):

`2\cdot x + 5 = 0`

`x = -(5)/(2)`

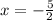
The critical point is
`-(5)/(2)`.

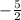As the second derivative is a constant function, we know that critical point leads to a minimum by Second Derivative Test, since
`f\left(-(5)/(2)\right) > 0`.

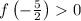Lastly, we find the remaining component associated with the critical point by direct evaluation of the function:

`f\left(-(5)/(2) \right) = \left(-(5)/(2) \right)^(2) + 5\cdot \left(-(5)/(2) \right) - 2`

`f\left(-(5)/(2) \right) = -(33)/(4)`

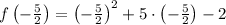
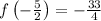
There are relative maxima.