A student takes two subjects A and B. Know that the probability of passing subjects A and B is 0.8 and 0.7 respectively. If you have passed subject A, the probability of passing…

Question

asked Mar 1, 2022 184k views

1 Answer

Osama · Answer 1 · 2022-03-07T23:25:36+0000

Answer:

0.64 = 64% probability that the student passes both subjects.

0.86 = 86% probability that the student passes at least one of the two subjects

Explanation:

Conditional Probability

We use the conditional probability formula to solve this question. It is

$P(B|A) = (P(A \cap B))/(P(A))$

In which

P(B|A) is the probability of event B happening, given that A happened.

$P(A \cap B)$ is the probability of both A and B happening.

P(A) is the probability of A happening.

In this question:

Event A: Passing subject A

Event B: Passing subject B

The probability of passing subject A is 0.8.

This means that
P(A) = 0.8

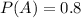
If you have passed subject A, the probability of passing subject B is 0.8.

This means that
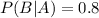
P(B|A) = 0.8

Find the probability that the student passes both subjects?

This is
$P(A \cap B)$ . So

$P(B|A) = (P(A \cap B))/(P(A))$

$P(A \cap B) = P(B|A)P(A) = 0.8*0.8 = 0.64$

0.64 = 64% probability that the student passes both subjects.

Find the probability that the student passes at least one of the two subjects

This is:

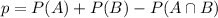
$p = P(A) + P(B) - P(A \cap B)$

Considering
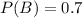P(B) = 0.7 , we have that:

$p = P(A) + P(B) - P(A \cap B) = 0.8 + 0.7 - 0.64 = 0.86$

0.86 = 86% probability that the student passes at least one of the two subjects