Answer:
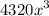
Explanation:
to solve binomials like this there's a way called binomial theorem given by

but for this question we need the following part
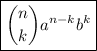
from the question we obtain that a,b and n is 3x,4 and 5 since we want to find the coefficient x³ k should be (5-3) = 2 so we have determined the variables now just substitute
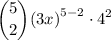
simplify which yields:
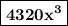
and we are done!