Given:
The function is:
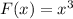
To find:
The function G(x) if the graph of F(x) can be compressed vertically and shifted to the right to produce the graph of G(x).
Solution:
The transformation is defined as
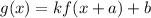 .... (i)
.... (i)
Where, k is stretch factor, a is horizontal shift and b is vertical shift.
If 0<k<1, then the graph compressed vertically by factor k and if k>1, then the graph stretch vertically by factor k.
If a>0, then the graph shifts a units left and if a<0, then the graph shifts a units right.
If b>0, then the graph shifts b units up and if b<0, then the graph shifts b units down.
It is given that F(x) can be compressed vertically and shifted to the right to produce the graph of G(x). So, the value of k must be lies between 0 and 1, and a<0.
In option A,
 and
and
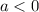 . So, this option is correct.
. So, this option is correct.
In option B,
 and
and
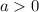 . So, this option is incorrect.
. So, this option is incorrect.
In option C,
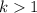 and
and
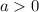 . So, this option is incorrect.
. So, this option is incorrect.
In option D,
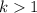 and
and
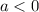 . So, this option is incorrect.
. So, this option is incorrect.
Therefore, the correct option is A.