1 Answer

Kelvin Chung · Answer 1 · 2022-08-14T07:48:36+0000

Given:

In the given figure
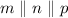$m\parallel n\parallel p$ .

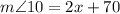
$m\angle 10=2x+70$

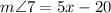
$m\angle 7=5x-20$

To find:

The
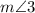$m\angle 3$ .

Solution:

If a transversal line intersect two parallel lines, then the alternate exterior angles are equal.

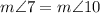$m\angle 7=m\angle 10$ (Alternate exterior angle)

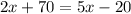
2x+70=5x-20

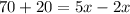
70+20=5x-2x

90=3x

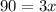
Divide both sides by 3.

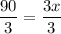
(90)/(3)=(3x)/(3)

30=x

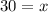
Now,

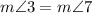$m\angle 3=m\angle 7$ (Corresponding angles)

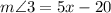
$m\angle 3=5x-20$

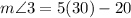
$m\angle 3=5(30)-20$

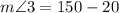
$m\angle 3=150-20$

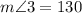
$m\angle 3=130$

Therefore, the measure of angle 3 is 130 degrees.

Please log in or register to add a comment.