Question

Find a, b, c, and d such that the cubic function f(x) = ax3 + bx? + cx + d satisfies the given conditions.

Relative maximum: (2,9)
Relative minimum: (4,3)
Inflection point: (3,6)
a =
b =
C=
d =

Answer 1

`\displaystyle f(x)=(3)/(2)x^3-(27)/(2)x^2+36x-21`

Where:

`\displaystyle a=(3)/(2), \, b=-(27)/(2), \, c=36, \text{and } d=-21`

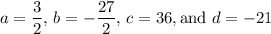
Explanation:

We are given a cubic function:

`f(x)=ax^3+bx^2+cx+d`

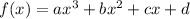
And we want to find a, b, c and d such that the function has a relative maximum at (2, 9); a relative mininum at (4, 3); and an inflection point at (3, 6).

Since the function has a relative maximum at (2, 9), this means that:

`f(2)=9=a(2)^3+b(2)^2+c(2)+d`

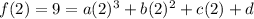
Simplify:

`8a+4b+2c+d=9`

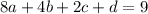
Likewise, since it has a relative minimum at (4, 3):

`f(4)=3=a(4)^3+b(4)^2+c(4)+d`

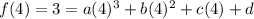
Simplify:

`64a+16b+4c+d=3`

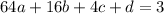
We can subtract the first equation from the second. So:

`(64a+16b+4c+d)-(8a+4b+2c+d)=(3)-(9)`

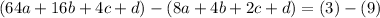
Simplify:

`56a+12b+2c=-6`

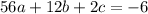
Divide both sides by two. Hence:

`28a+6b+c=-3`

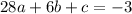
Relative minima occurs only at the critical points of a function. That is, it occurs whenever the first derivative equals zero.

Find the first derivative. We can treat a, b, c and d as constant. Hence:

`f'(x)=3ax^2+2bx+c`

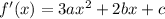
Since it has a minima at (2, 9), it means that:

`f'(2)=3a(2)^2+2b(2)+c=0`

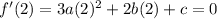
Thus:

`12a+4b+c=0`

(We will only need one of the two points to complete the problem.)

Inflection points occurs whenever the second derivative of a function equals zero. Find the second derivative:

`f''(x)=6ax+2b`

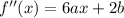
Since there is a inflection point at (3, 6):

`18a+2b=0\Rightarrow 9a+b=0`

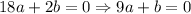
Solve for b:

`b=-9a`

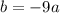
Substitute this into the above equation:

`12a+4(-9a)+c=0`

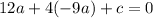
Solve for c:

`c=24a`

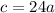
Substitute b and c into the previously acquired equation:

`28a+6(-9a)+(24a)=-3`

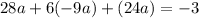
Solve for a:

`\displaystyle -2a=-3\Rightarrow a=(3)/(2)`

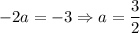
Solve for b and c:

`\displaystyle b=-9\left((3)/(2)\right)=-(27)/(2)\text{ and } c=24\left((3)/(2)\right)=36`

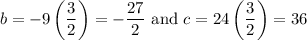
Using either the very first or second equation, solve for d:

`\displaystyle 8\left((3)/(2)\right)+4\left(-(27)/(2)\right)+2(36)+d=9`

Hence:

`d=-21`

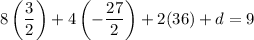
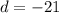
Hence, our function is:

`\displaystyle f(x)=(3)/(2)x^3-(27)/(2)x^2+36x-21`