Question

(2x² - 5x-3)/ (x-3)
DIvide the polynomials

Answer 1

2x + 1

Explanation:

`((2x² - 5x-3))/((x - 3))`

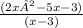
Factor out 2x² - 5x-3

`((2x + 1)(x - 3))/(x - 3)`

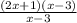
divide x - 3 by x - 3

=> 2x + 1

Or another step

Step by Step Solution

STEP

1

:

Equation at the end of step 1

STEP

2

:

2x² - 5x - 3/ x - 3

Trying to factor by splitting the middle term

2.1 Factoring 2x² - 5x - 3

The first term is, 2x² its coefficient is 2 .

The middle term is, -5x its coefficient is -5 .

The last term, "the constant", is -3

Step-1 : Multiply the coefficient of the first term by the constant 2 • -3 = -6

Step-2 : Find two factors of -6 whose sum equals the coefficient of the middle term, which is -5 .

-6 + 1 = -5 That's it

Step-3 : Rewrite the polynomial splitting the middle term using the two factors found in step 2 above, -6 and 1

2x² - 6x + 1x - 3

Step-4 : Add up the first 2 terms, pulling out like factors :

2x • (x-3)

Add up the last 2 terms, pulling out common factors :

1 • (x-3)

Step-5 : Add up the four terms of step 4 :

(2x+1) • (x-3)

Which is the desired factorization

Canceling Out :

2.2 Cancel out (x-3) which appears on both sides of the fraction line.

Final result :

2x + 1