Given:
The expression is:
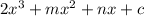
It leaves the same remainder when divided by x -2 or by x+1.
To prove:
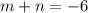
Solution:
Remainder theorem: If a polynomial P(x) is divided by (x-c), thent he remainder is P(c).
Let the given polynomial is:
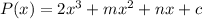
It leaves the same remainder when divided by x -2 or by x+1. By using remainder theorem, we can say that
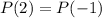 ...(i)
...(i)
Substituting
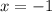 in the given polynomial.
in the given polynomial.
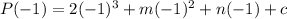

Substituting
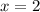 in the given polynomial.
in the given polynomial.


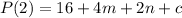
Now, substitute the values of P(2) and P(-1) in (i), we get


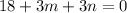
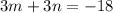
Divide both sides by 3.
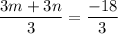
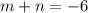
Hence proved.