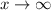Given:
The given function is:
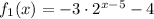
The graph of the function is given.
To find:
The end behavior of the given function.
Solution:
We have,
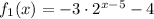
From the given graph it is clear that the function approaches to -4 at x approaches negative infinite and the function approaches to negative infinite at x approaches infinite.
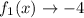 as
as
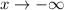
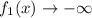 as
as
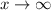
Therefore, the end behaviors of the given function are:
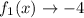 as
as
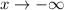
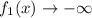 as
as