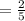Answer:
The correct answer is "
 ". A further solution is provided below.
". A further solution is provided below.
Explanation:
According to the question,
The probability of getting a 5 will be:
=
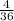
=

The probability of getting a 7 will be:
=

=
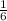
The probability of not a 5 nor a 7 will be:
=
![1-[(4)/(36) +(4)/(36) ]](https://img.qammunity.org/2022/formulas/mathematics/college/e5sa1scideqyz1q6w872w10063h0x119r2.png)
=
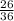
=
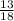
Now,
For roll of 2 dice,
⇒
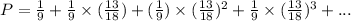
![=(1)/(9) [1+(13)/(18) +(13^2)/(18^2) +(13^3)/(18^3) +...]](https://img.qammunity.org/2022/formulas/mathematics/college/jlu7gqug67s8botppvh1ovp3i2r8w84ra7.png)
![=(1)/(9) [(1)/(1-(13)/(18) ) ]](https://img.qammunity.org/2022/formulas/mathematics/college/h2n1lz96887vml3hn6r8tx8bdh1nv2y091.png)
![=(1)/(9) [{(1)/((5)/(8) ) ]](https://img.qammunity.org/2022/formulas/mathematics/college/jgw4t3ipfdnhu50drlug1ji9ifj6ojz76r.png)