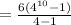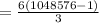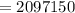Answer:
2097150
Explanation:
GIVEN :-
- First term of G.P. = 6
- Forth term of G.P. = 384
TO FIND :-
- Sum of first 10 terms of the G.P.
CONCEPT TO BE USED IN THIS QUESTION :-
Geometric Progression :-
- It's a sequence in which the successive terms have same ratio.
- General form of a G.P. ⇒ a , ar , ar² , ar³ , ....... [where a = first term ; r = common ratio between successive terms]
- Sum of 'n' terms of a G.P. ⇒
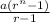 .
.
[NOTE :-
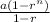 can also be the formula for "Sum of n terms of G.P." because if you put 'r' there (assuming r > 0) you'll get negative value in both the numerator & denominator from which the negative sign will get cancelled from the numerator & denominator. YOU'LL BE GETTING THE SAME VALUE FROM BOTH THE FORMULAES.]
can also be the formula for "Sum of n terms of G.P." because if you put 'r' there (assuming r > 0) you'll get negative value in both the numerator & denominator from which the negative sign will get cancelled from the numerator & denominator. YOU'LL BE GETTING THE SAME VALUE FROM BOTH THE FORMULAES.]
SOLUTION :-
Let the first term of the G.P. given in the question be 'a' and the common ratio between successive terms be 'r'.
⇒ a = 6
It's given that forth term is 384. So from "General form of G.P." , it can be stated that :-
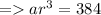
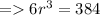
Divide both the sides by 6.
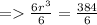

![=> r = \sqrt[3]{64} = 4](https://img.qammunity.org/2022/formulas/mathematics/high-school/jqg9q0kxzqbpsv4d5t6hc4x61ab9pu16r2.png)
Sum of first 10 terms