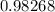Question

The head of maintenance at XYZ Rent-A-Car believes that the mean number of miles between services is 3408 miles, with a variance of 249,001. If he is correct, what is the probability that the mean of a sample of 36 cars would differ from the population mean by less than 198 miles

Answer 1

`0.98268`

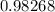
Explanation:

We are given that

Mean,
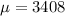`\mu=3408`miles

Variance,
`\sigma^2=249001`

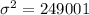
We have to find the probability that the mean of a sample of 36 cars would differ from the population mean by less than 198 miles.

n=36

`P(|\bar{x}-3408}|<198)=P(3408-198<\bar{x}<198+3408)`

=
`P(3210<\bar{x}<3606)`

=
`P(\frac{3210-3408}{\sqrt{(249001)/(36)}}<\frac{\bar{x}-\mu}{\sqrt{(variance)/(n)}}<\frac{3606-3408}{\sqrt{(249001)/(36)}}`

`=P(-2.38<Z<2.38)`

`=P(Z<2.38)-P(Z<-2.38)`

`=0.99134-0.00866`

=
`0.98268`

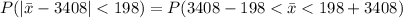
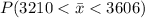
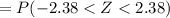
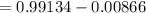
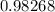
Hence, the probability that the mean of a sample of 36 cars would differ from the population mean by less than 198 miles=
`0.98268`