Answer:
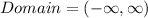
![Range = (-\infty, 4]](https://img.qammunity.org/2022/formulas/mathematics/high-school/s4a5rf3c8x3p6h0w5k6uw7qhdu054jjgcf.png)
Increasing interval is:
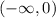
Decreasing interval is:

Constant at no interval
Explanation:
Given
See attachment for graph
Solving (a): The domain
From, the attached graph, we have:
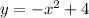
The degree of the polynomial (i.e 2) is even.
Hence, the domain is the set of all real numbers, i.e.
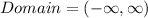
Solving (b): The range
The curve of
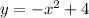 opens downward, and the maximum is:
opens downward, and the maximum is:

This means that the minimum is:
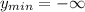
Hence, the range of the set is:
![Range = (-\infty, 4]](https://img.qammunity.org/2022/formulas/mathematics/high-school/s4a5rf3c8x3p6h0w5k6uw7qhdu054jjgcf.png)
Solving (c): Interval where the function increases/decreases/constant
In (a), we have:
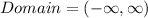
Split to 2 (at vertex x = 0)
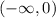 and
and

So:
The increasing interval is:
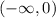
The decreasing interval is:

The function has a tangent at
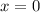 but at no interval, was the function constant
but at no interval, was the function constant