Question

Consider the cylindrical weir of diameter 3 m and length 6m. If the fluid on the left has a specific gravity of 0.8, find the magnitude and direction of the resultant force

Answer 1

This question is incomplete, the complete question is;

Consider the cylindrical weir of diameter 3m and length 6m. If the fluid on the left has a specific gravity of 1.6 and on the right has a specific gravity of 0.8, Find the magnitude and direction of the resultant force.

Answer:

- the magnitude of the resultant force is 557.32 kN

- the direction of resultant force is 48.29°

Step-by-step explanation:

Given the data in the question and the diagram below,

First we work on the force on the left hand side.

Left Horizontal

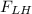`F_{LH` = βgAr

here, h = 3/2 = 1.5 m, β = 1.6, g = 9.81 m/s², A = 3 m × 6 m = 18 m²

we substitute

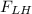`F_{LH` = βgAh = ( 1.6 × 1000 ) × 9.81 × 18 × 1.5 = 423792 N

Left Vertical

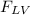`F_{LV` = ( βgπh² / 2 ) × W

we substitute

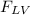`F_{LV` = [ ( ( 1.6 × 1000 ) × 9.81 × π(1.5)² ) / 2 ] × 6 = 332845.458 N

Now we go to the right hand side

Right Horizontal

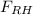`F_{RH` = βgAh

here, h' = 1.5/2 = 0.75 m, β = 0.8, g = 9.81 m/s², A = 1.5 m × 6 m = 9 m²

we substitute

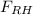`F_{RH` = ( 0.8 × 1000 ) × 9.81 × 9 × 0.75 ) = 52974 N

Right Vertical

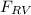`F_{RV` = ( βgπh² / 4 ) × W

we substitute

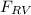`F_{RV` = [ ( ( 0.8 × 1000 ) × 9.81 × π(1.5)² ) / 4 ] × 6 = 83211.36 N

Hence

Fx =
`F_{LH` -
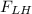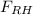`F_{RH` = 52974 N - 423792 N = 370818 N

Fy =
`F_{LV` +
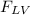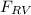`F_{RV` = 332845.458 N + 83211.36 N = 416056.818 N

R = √( Fx² + Fy² ) = √[ (370818 N)² + (416056.818 N)² ] = 557323.3 N

R = 557.32 kN

Therefore, the magnitude of the resultant force is 557.32 kN

Direction of resultant force;

tanθ = Fy / Fx

we substitute

tanθ = 416056.818 N / 370818 N

tanθ = 1.121997

θ = tan⁻¹( 1.121997 )

θ = 48.29°

Therefore, the direction of resultant force is 48.29°