Question

A ball is thrown into the air with an upward velocity of 24 ft/s. Its height h in feet after t seconds is given by the function h = –16t2 + 24t + 7. a. In how many seconds does the ball reach its maximum height? Round to the nearest hundredth if necessary. b. What is the ball’s maximum height?

Answer 1

Explanation:

Since you have this categorized under college math, I'm going to go out on a limb here and assume you're in calculus. We will solve using the position function and its first derivative (velocity) to solve. Remember that at an object's max height, the velocity is 0.

If the position function is

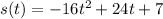`s(t)=-16t^2+24t+7` the first derivative, velocity, is

v(t) = -32t + 24. Set this equal to 0 to find the time when the object is at its max height:

0 = -32t + 24 and

-24 = -32t so

t = .75 seconds. Now we can plug that time into the position function to find where it is at that time. This "where" will be the max height:

s(.75) =
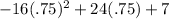`-16(.75)^2+24(.75)+7` so

s(.75) = 16 feet