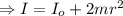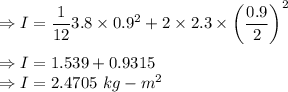Question

A uniform steel rod of length 0.9 m and mass 3.8 kg has two point masses of 2.3 kg each at the two ends. Calculate the moment of inertia of the system about an axis perpendicular to the rod, and passing through its center.

Answer 1

Answer:
`2.4705\ kg.m^2`

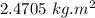
Step-by-step explanation:

Given

length of the rod is L=0.9 m

Mass of the rod m=3.8 kg

Point masses has mass of m=2.3 kg

Moment of Inertia of the rod about the center is

`\Rightarrow I_o=(1)/(12)ML^2`

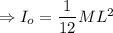
Moment of inertia of combined system is the sum of rod and two point masses.

`\Rightarrow I=I_o+2mr^2`

`\Rightarrow I=(1)/(12)3.8* 0.9^2+2* 2.3* \left((0.9)/(2)\right)^2\\\\\Rightarrow I=1.539+0.9315\\\Rightarrow I=2.4705\ kg-m^2`