Question

four equal magnitude point charges 3 microcoulomb is placed at the corners of a square that is 40cm inside find the force on any one of the charges ​

Answer 1

Approximately
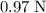`0.97\; \rm N`. This force would point away from the center of the square (to the left at
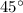`45^\circ` above the horizontal direction.)

Step-by-step explanation:

Coulomb's constant:
`k \approx 8.98755 * 10^(-9)\; \rm N \cdot m^(2) \cdot C^(-2)`.

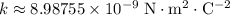By Coulomb's Law, the electrostatic force between two point charges
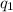`q_1` and
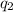`q_2` that are separated by
`r` (vacuum) would be:

`\displaystyle F = (k \cdot q_1 \cdot q_2)/(r^2)`.

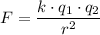Consider the charge on the top-left corner of this square.

Apply Coulomb's Law to find the electrostatic force between this charge and the charge on the lower-left corner.

Convert quantities to standard units:

`q_1 = q_2 = 3 * 10^(-6)\; \rm C`.

`r = 0.40\; \rm m`.

`\begin{aligned}F &= (k \cdot q_1 \cdot q_2)/(r^2) \\ &\approx (8.98755 * 10^(-9)\; \rm N \cdot m^(2) \cdot C^(-2) * (3 * 10^(-6)\; \rm C)^(2))/((0.40\; \rm m)^(2)) \\ &\approx 0.506\; \rm N\end{aligned}`.

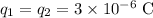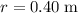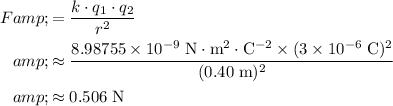As the two charges are of the same sign, the electrostatic force on each charge would point away from the other charge. Hence, for the charge on the top-left corner of the square, the electrostatic force from the charge below it would point upwards.

Similarly, the charge to the right of this charge would exert an electrostatic force with the same magnitude (approximately
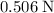`0.506\; \rm N`) that points leftwards.

For the charge to the lower-right of the top-left charge,
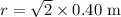`r = √(2) * 0.40\; \rm m`. Therefore:

`\begin{aligned}F &= (k \cdot q_1 \cdot q_2)/(r^2) \\ &\approx (8.98755 * 10^(-9)\; \rm N \cdot m^(2) \cdot C^(-2) * (3 * 10^(-6)\; \rm C)^(2))/((√(2) * 0.40\; \rm m)^(2)) \\ &\approx 0.253 \; \rm N\end{aligned}`.

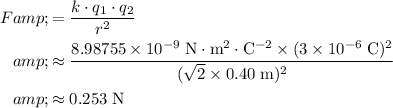This force would point to the top-left of the top-left charge, which is
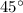`45^\circ` above the horizontal direction. Decompose this force into two components that are normal to one another:

• Horizontal component: approximately
  `\sin(45^\circ) * 0.253\; \rm N \approx 0.179\; \rm N`.
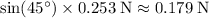• Vertical component: approximately
  `\cos(45^\circ) * 0.253\; \rm N \approx 0.179\; \rm N`

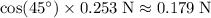
Consider the net force on the top-left charge in two components:

• Horizontal component: approximately
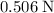  `0.506\; \rm N` from the charge on the top-right corner and approximately
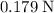  `0.179\; \rm N` from the charge on the lower-right corner. Both components point to the left-hand side.
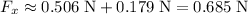  `F_x \approx 0.506\; \rm N + 0.179\; \rm N = 0.685\;\rm N` (to the left).

• Vertical component: approximately
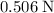  `0.506\; \rm N` from the charge on the lower-left corner and approximately
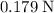  `0.179\; \rm N` from the charge on the lower-right corner. Both components point upwards.
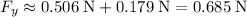  `F_y \approx 0.506\; \rm N + 0.179\; \rm N = 0.685\;\rm N` (upward).

Combine these two components to find the magnitude of the net force on this charge:

`\begin{aligned}F &= \sqrt{{F_x}^(2) + {F_y}^(2)} \\ &\approx √(0.685^2 + 0.685^2 )\; \rm N \\ &\approx 0.97\; \rm N\end{aligned}`.

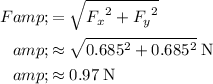This force would point to the top-left of this charge (also at
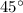`45^\circ` above the horizontal direction, away from the center of the square) because its horizontal and vertical components have the same magnitude.