Question

Graph the solution of the inequality 3/7(35x-14)<_ 21x/2+3

Answer 1

You'll have a closed circle at x = 2, and shading to the left

See the diagram below

=========================================================

Step-by-step explanation:

The fractions here are 3/7 and 21/2. The denominators of which are 7 and 2 respectively. The LCD is 7*2 = 14.

If we multiply both sides by 14, then this will clear out the denominators and make the fractions go away.

• 14*(3/7) = (14*3)/7 = 42/7 = 6
• 14*(21/2) = (14*21)/2 = 294/2 = 147

So if we multiplied both sides by 14, then we have these steps

`(3)/(7)(35x-14) \le (21x)/(2)+3\\\\14*(3)/(7)(35x-14) \le 14*\left((21x)/(2)+3\right)\\\\14*(3)/(7)(35x-14) \le 14*\left((21x)/(2)\right)+14*\left(3\right)\\\\6(35x-14) \le 147x+42\\\\`

--------------------------

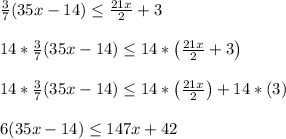
Let's isolate x

`6(35x-14) \le 147x+42\\\\6(35x)+6(-14) \le 147x+42\\\\210x-84 \le 147x+42\\\\210x-147x \le 42+84\\\\63x \le 126\\\\x \le 126/63\\\\x \le 2\\\\`

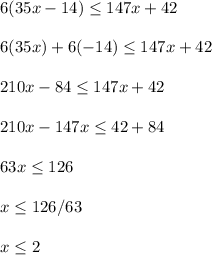
The graph of this will consist of a closed or filled in circle at x = 2. We shade to the left to represent numbers smaller than 2.

So either x = 2 or x < 2.

If we used an open hole at 2, then we wouldn't be including 2 (but we want to include this endpoint).

See the diagram below.