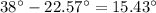Answer:
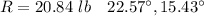
Explanation:
Given
Two forces of 9 and 13 lbs acts
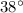 angle to each other
angle to each other
The resultant of the two forces is given by
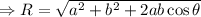
Insert the values
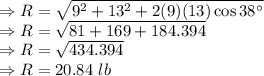
Resultant makes an angle of

So, the resultant makes an angle of
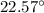 with 9 lb force
with 9 lb force
Angle made with 13 lb force is