Question

What are the coordinates for the angle π/4 on tge unit circle

Answer 1

Answer: Both x and y are
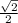`(√(2))/(2)` which is the same as
`(1)/(√(2))`

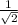
In other words, the point
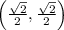`\left( (√(2))/(2), (√(2))/(2) \right)` is on the unit circle for the angle pi/4 radians. This point is equivalent to
`\left( (1)/(√(2)), (1)/(√(2))\right)`

==============================================

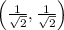
Step-by-step explanation:

The angle pi/4 radians is equivalent to 45 degrees. Draw out a 45-45-90 triangle with hypotenuse 1, and you'll find the congruent legs are each
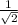`(1)/(√(2))` units long (apply the pythagorean theorem). If you apply the sine and cosine ratios, you'll get the answer shown above.

Recall that

• x = cos(theta)
• y = sin(theta)

and also

• cos = adjacent/hypotenuse
• sin = opposite/hypotenuse

The pythagorean theorem is a^2+b^2 = c^2.