Question

Give the values of A, B, and C needed to write the equation's general form.

(5 + x)(5 - x) = 7

1. A = 1; B = 0; C = -18
2. A= -1; B = 0; C = 25
3. A = 25; B = 0; C = -1

Answer 1

Given:

The equation is:

`(5+x)(5-x)=7`

To find:

The value of A, B and C for the equation's general form.

Solution:

We have,

`(5+x)(5-x)=7`

Using distribution property, we get

`(5)(5)+(5)(-x)+(x)(5)+(x)(-x)=7`

`25-5x+5x-x^2=7`

`25-x^2=7`

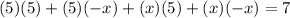
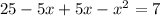
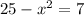
Taking all terms on one side, we get

`25-x^2-7=0`

`-x^2+18=0`

`-(x^2-18)=0`

`x^2-18=0`

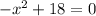
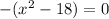
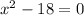
On comparing this equation with the general form of a quadratic equation
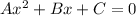`Ax^2+Bx+C=0`, we get

`A=1`

`B=0`

`C=-18`

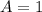
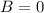
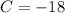
Therefore, the correct option is 1.