Question

asked Nov 5, 2022 145k views

1 Answer

Sherali Turdiyev · Answer 1 · 2022-11-11T14:37:35+0000

Given:

The vertices of a triangle are D(1,5), O(7,-1) and G(3,-1).

To find:

The perpendicular bisector of line segment DO.

Solution:

Midpoint formula:

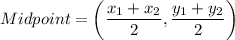
$Midpoint=\left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)$

The midpoint of DO is:

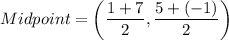
$Midpoint=\left((1+7)/(2),(5+(-1))/(2)\right)$

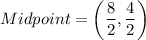
$Midpoint=\left((8)/(2),(4)/(2)\right)$

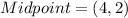
$Midpoint=\left(4,2\right)$

Therefore, the midpoint of DO is (4,2).

Slope formula:

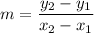
m=(y_2-y_1)/(x_2-x_1)

Slope of DO is:

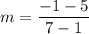
m=(-1-5)/(7-1)

m=(-6)/(6)

m=-1

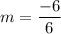
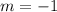
Therefore, the slope of DO is -1.

We know that the product of slopes of two perpendicular line is -1.

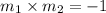
m_1* m_2=-1

m_1* (-1)=-1

m_1=1

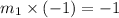
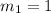
The slope of perpendicular bisector is 1 and it passes through the point (4,2). So, the equation of the perpendicular bisector of DO is:

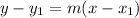
y-y_1=m(x-x_1)

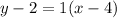
y-2=1(x-4)

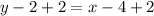
y-2+2=x-4+2

y=x-2

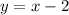
Therefore, the equation of the perpendicular bisector of DO is
.

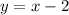Please log in or register to add a comment.