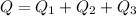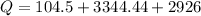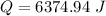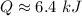Question

The following physical constants are for water, H2O.

The specific heat capacity of the solid = 2.09 J/g oC
The specific heat capacity of the liquid = 4.18 J/g oC
The specific heat capacity of the vapor = 2.09 J/g oC
∆Hfus = 6.02 kJ/mol; ∆Hvap = 40.7 kJ/mol Freezing point = 0.0oC; Boiling point = 100.0oC
How much heat(in kJ) is required to warm 10.0 grams of ice at -5.0oC to a temperature of 70.0oC?

Answer 1

`Q\approx6.4~kJ`

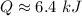
Step-by-step explanation:

Quantity of heat required by 10 gram of ice initially warm it from -5°C to 0°C:

`Q_1=m.C_s.\Delta T`

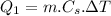
here;

mass, m = 10 g

specific heat capacity of ice,
`C_s=2.09~J.g^(-1).^(\circ)C^(-1)`

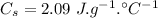
change in temperature,
`\Delta T=(5-0)=5^(o)C`

`Q_1=10*2.09* 5`

`Q_1=104.5~J`

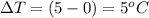
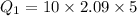
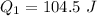
Amount of heat required to melt the ice at 0°C:

`Q_2=m.\Delta H_(fus)`

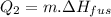
where,
`\Delta H_(fus)=6020~J/mol`

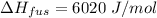
we know that no. of moles is = (wt. in gram)
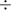`/` (molecular mass)

`Q_2=(10)/(18) * 6020`

`Q_2=3344.44~J`

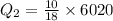
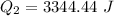
Now, the heat required to bring the water to 70°C from 0°C:

`Q_3=m.C_L.\Delta T`

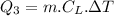
specific heat of water,
`C_L=4.18~J/g/^oC`

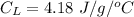
change in temperature,
`\Delta T=(70-0)=70^oC`

`Q_3=10* 4.18* 70`

`Q_3=2926~J`

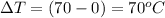
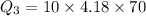
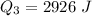
Therefore the total heat required to warm 10.0 grams of ice at -5.0°C to a temperature of 70.0°C:

`Q=Q_1+Q_2+Q_3`

`Q=104.5+3344.44+2926`

`Q=6374.94~J`

`Q\approx6.4~kJ`