Given:
The number of ribbons it can sell each week, x, is related to the price p per ribbon by the equation:
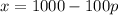
To find:
The selling price if the company wants the weekly revenue to be $1,600.
Solution:
We know that the revenue is the product of quantity and price.

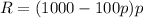
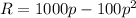
We need to find the value of p when the value of R is $1600.
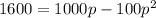
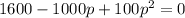

Divide both sides by 100.
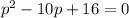
Splitting the middle term, we get

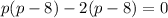

Using zero product property, we get
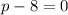 or
or
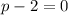
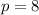 or
or
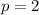
Therefore, the smaller value of p is $2 and the larger value of p is $8.